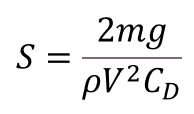はじめに
パラシュートはロケットを安全に回収するための重要な要素です．その大きさが変われば，空気抵抗が変わり，安全に回収できるのかどうかに大きく影響します．
なんとなくこんな形かな？と職人技で作ることもできますが，
対象物の重さと落下の速度を設定して，パラシュートの大きさがどれくらい必要か，定量的に計算する方法を前提の基礎知識から流体力学の理論式を用いて解説します．
ニュートンの第2法則 (終端速度)
当然，地球には重力があります．また，大気があるので空気抵抗を受けます．パラシュートを展開した後，だんだんスピードが速くなっていきますが，時間が経つと空気抵抗によって一定速度以上にならずに等速運動になります．これを終端速度(terminal velocity)といいます．等速運動ということは，加速度が０ということなのでニュートンの第2法則より（運動方程式より）力が釣り合っているということになります．
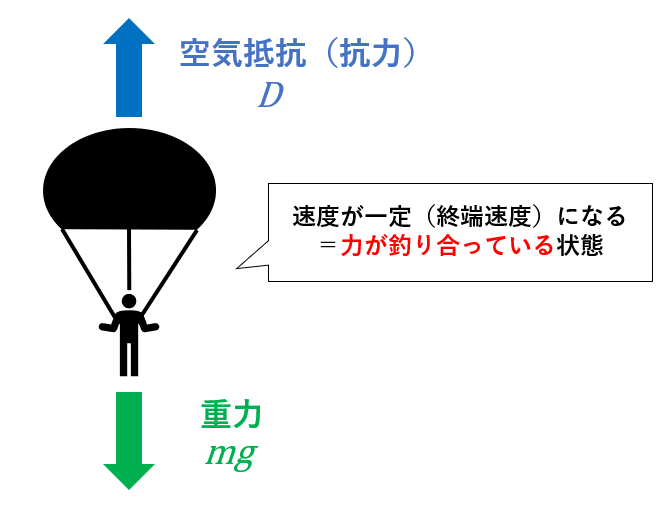
また，ここで空気抵抗Dは以下の式で表すことができます．
ここでの代表面積Sはパラシュートの投影面積（真上から光を当てた時に地面にできる影の面積）です．
このSがパラシュートを設計するうえで知りたい値になります！
（Sがパラシュートの大きさを決定する値になります）
先ほどの式にDの式を代入すると，終端速度Vは以下の式で表されます．
ここで，
空気の密度ρは常温20℃で1.204[kg/m3],重力加速度gは9.81 [m/s2]とする．
抵抗係数は物体の形状に依存するので，ネット検索などして自作するパラシュートの形状と同じ形状のものを代入して下さい．論文などを探すと載っています．典型的なパラシュートの抗力係数は1.75とNASAのサイトに掲載されていました．
Typical values of drag coefficient for a parachute is about 1.75
https://www.grc.nasa.gov/www/k-12/VirtualAero/BottleRocket/airplane/rktvrecv.html
設計してみよう（実用例）
実用例として，以下の条件で必要なパラシュートの大きさを計算してみようと思います．
落下物の重さm 500g (0.5kg)
落下速度V 6m/s
空気の密度ρ 1.204kg/m3
重力加速度g 9.81m/s2
抗力係数 1.75
必要なパラシュートの投影面積Sは以下の式で計算できる．（先ほどの終端速度の式を変形しただけ）
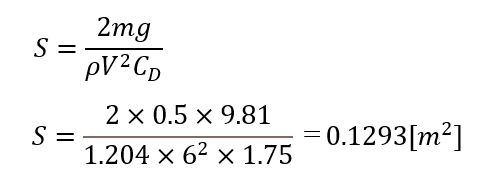
投影の形状が円形だとすると，その直径dは以下の式で計算できる．
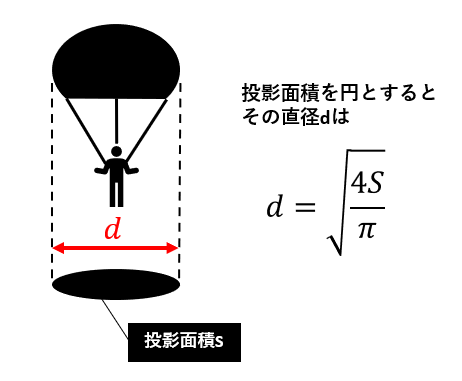
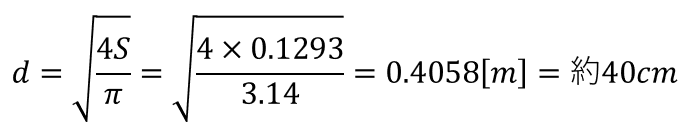
この直径ｄはあくまで落下中にパラシュートが半球形状になっている時の影の直径なので，実際にパラシュートを製作するときの直径Ｌは以下の式で求める．
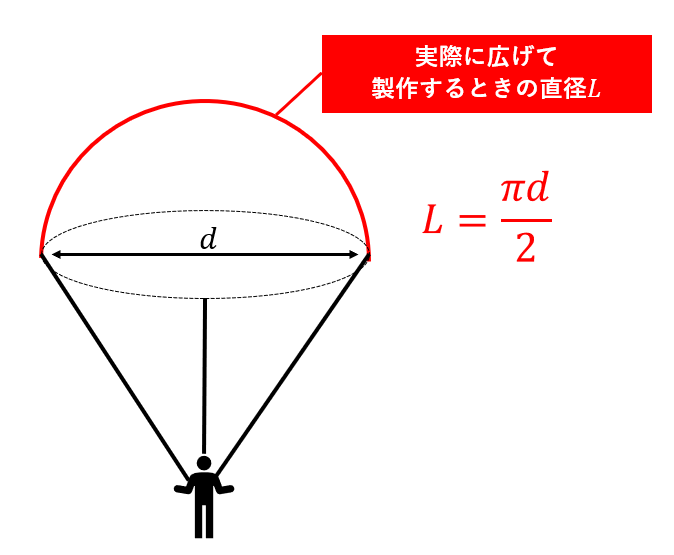
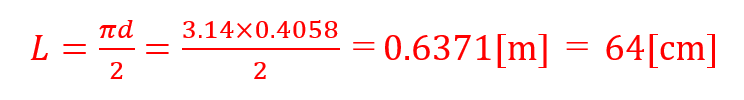
したがって，この場合は直径64cmの大きさの円を材料（布やビニールなど）から切り出して作れば，要求通りの終端速度になるパラシュートを製作できることになる．
皆さんもぜひ！理論計算を用いて設計したパラシュートを作ってみてください！
